DiGraphWrapper Class Reference

Wraps the DiGraph class with type annotations for the nodes. More...

Inheritance diagram for DiGraphWrapper:

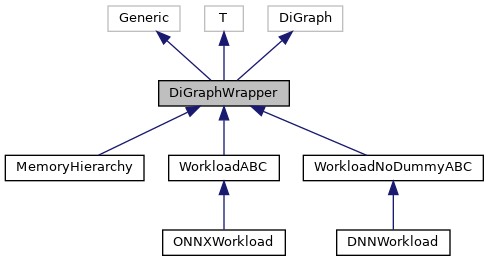
Collaboration diagram for DiGraphWrapper:

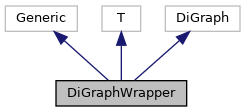
Public Member Functions
list[tuple[T, T]]	in_edges (self, T node, Literal[False] data)
list[tuple[T, T, dict[str, Any]]]	in_edges (self, T node, Literal[True] data)
list[tuple[T, T]]	in_edges (self, T node)
list[tuple[T, T]]|list[tuple[T, T, dict[str, Any]]]	in_edges (self, T node, bool data=False)
list[tuple[T, T, dict[str, Any]]]	out_edges (self, T node, Literal[True] data)
list[tuple[T, T]]	out_edges (self, T node, Literal[False] data)
list[tuple[T, T]]	out_edges (self, T node)
list[tuple[T, T]]|list[tuple[T, T, dict[str, Any]]]	out_edges (self, T node, bool data=False)
Iterator[tuple[T, int]]	in_degree (self)
Iterator[tuple[T, int]]	out_degree (self, Literal[None] node)
Iterator[tuple[T, int]]	out_degree (self)
int	out_degree (self, T node)
int|Iterator[tuple[T, int]]	out_degree (self, T|None node=None)
Iterator[T]	successors (self, T node)
Iterator[T]	predecessors (self, T node)
Iterator[T]	topological_sort (self)
None	add_node (self, T node)
None	add_nodes_from (self, Sequence[T] node)
None	remove_nodes_from (self, Iterator[T] nodes)
None	add_edge (self, T edge_from, T edge_to)
None	add_edges_from (self, Sequence[tuple[T, T]|tuple[T, T, Any]] edges)
Iterator[list[T]]	all_simple_paths (self, T producer, T consumer)
list[T]	shortest_path (self, T producer, T consumer)
list[T]	node_list (self)
T	get_node_with_id (self, int node_id)

Detailed Description

Wraps the DiGraph class with type annotations for the nodes.

Member Function Documentation

add_edge()

None add_edge	(		self,
		T	edge_from,
		T	edge_to
	)

Here is the caller graph for this function:

add_edges_from()

None add_edges_from	(		self,
		Sequence[tuple[T, T] | tuple[T, T, Any]]	edges
	)

Here is the caller graph for this function:

add_node()

None add_node	(		self,
		T	node
	)

Here is the caller graph for this function:

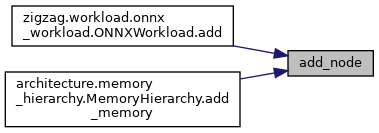
add_nodes_from()

None add_nodes_from	(		self,
		Sequence[T]	node
	)

all_simple_paths()

Iterator[list[T]] all_simple_paths	(		self,
		T	producer,
		T	consumer
	)

get_node_with_id()

T get_node_with_id	(		self,
		int	node_id
	)

Here is the call graph for this function:

in_degree()

Iterator[tuple[T, int]] in_degree

(

self

)

Here is the caller graph for this function:

in_edges() [1/4]

list[tuple[T, T]] in_edges	(		self,
		T	node
	)

Here is the call graph for this function:

in_edges() [2/4]

list[tuple[T, T]] | list[tuple[T, T, dict[str, Any]]] in_edges	(		self,
		T	node,
		bool	data = False
	)

Here is the call graph for this function:

in_edges() [3/4]

list[tuple[T, T]] in_edges	(		self,
		T	node,
		Literal[False]	data
	)

Here is the caller graph for this function:

in_edges() [4/4]

list[tuple[T, T, dict[str, Any]]] in_edges	(		self,
		T	node,
		Literal[True]	data
	)

Here is the call graph for this function:

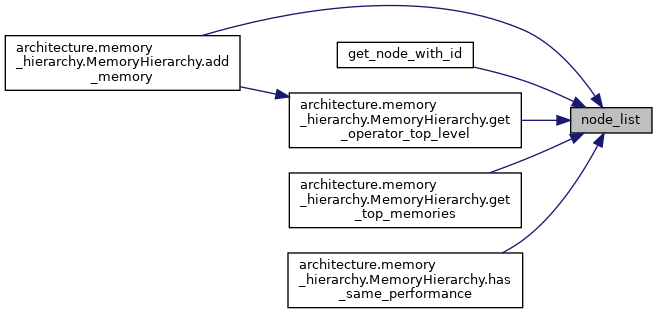
node_list()

list[T] node_list

(

self

)

Here is the caller graph for this function:

out_degree() [1/4]

Iterator[tuple[T, int]] out_degree

(

self

)

Here is the call graph for this function:

Here is the caller graph for this function:

out_degree() [2/4]

Iterator[tuple[T, int]] out_degree	(		self,
		Literal[None]	node
	)

Here is the caller graph for this function:

out_degree() [3/4]

int out_degree	(		self,
		T	node
	)

Here is the call graph for this function:

Here is the caller graph for this function:

out_degree() [4/4]

int | Iterator[tuple[T, int]] out_degree	(		self,
		T | None	node = None
	)

Here is the call graph for this function:

Here is the caller graph for this function:

out_edges() [1/4]

list[tuple[T, T]] out_edges	(		self,
		T	node
	)

Here is the call graph for this function:

out_edges() [2/4]

list[tuple[T, T]] | list[tuple[T, T, dict[str, Any]]] out_edges	(		self,
		T	node,
		bool	data = False
	)

Here is the call graph for this function:

out_edges() [3/4]

list[tuple[T, T]] out_edges	(		self,
		T	node,
		Literal[False]	data
	)

Here is the call graph for this function:

out_edges() [4/4]

list[tuple[T, T, dict[str, Any]]] out_edges	(		self,
		T	node,
		Literal[True]	data
	)

Here is the caller graph for this function:

predecessors()

Iterator[T] predecessors	(		self,
		T	node
	)

remove_nodes_from()

None remove_nodes_from	(		self,
		Iterator[T]	nodes
	)

shortest_path()

list[T] shortest_path	(		self,
		T	producer,
		T	consumer
	)

successors()

Iterator[T] successors	(		self,
		T	node
	)

topological_sort()

Iterator[T] topological_sort

(

self

)

Here is the caller graph for this function:

---

The documentation for this class was generated from the following file:

• /home/runner/work/zigzag/zigzag/zigzag/utils.py